neural_net.py에 코드를 채워 넣고 two_layer_net.ipynb를 실행 한 뒤에, 그 결과를 확인하고, 하이퍼 파라미터를 조정하는 과제이다. 이를 위해 skeleton code와 dataset을 다운로드 한 뒤에 jupyter notebook에서 아래와 같이 환경 설정을 완료한 뒤에 과제를 수행했다. 전체적으로 이미지의 화질이 좋지 않은 부분은 양해 부탁한다. 좀더 자세히 보고싶다면 첨부된 파일을 참조하기 바란다.
전체 코드 파일은 아래에 첨부하며, 과제 중에서 직접 채워 넣어야 하는 부분에 대한 설명을 이번 포스팅에서 작성하도록 한다.
<Code Analysis>
<1> neural_net.py
4개의 함수의 빈 부분의 코드를 채워 넣어 완성한다.
(1) def __init__(self, input_size, hidden_size, output_size, std=1e-4):
Weight를 작은 값으로, bias를 0으로 초기화하는 함수이다. 각 weight와 bias의 형태는 아래와 같다.

# Input_size: input data의 dimension(==D)
# Hidden_size: hidden layer의 뉴런 사이즈
# Output_size: class의 수(==C)
(2) def loss(self, X, y=None, reg=0.0):
Loss와 gradient를 계산하는 함수이다. X와 y의 형태는 아래와 같다. y = None이면 (N, C)의 score를 반환한다. 아니면 data loss와 regularization loss를 반환한다.
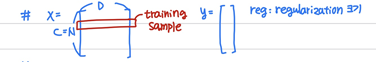
# Compute the forward pass
scores = None
##########################################################################
# TODO: Perform the forward pass, computing the class scores for the input. #
# Store the result in the scores variable, which should be an array of #
# shape (N, C). #
##########################################################################
z = np.dot(X, W1) + b1 # (N, num_hidden)
h = np.maximum(z, 0) # ReLU
scores = np.dot(h , W2) + b2
##########################################################################
# END OF YOUR CODE #
##########################################################################
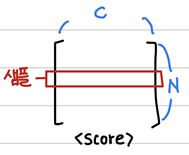
N은 샘플의 개수를 나타낸다. D는 input data의 feature의 개수를 나타낸다. H는 hidden layer의 뉴런의 개수를 나타낸다. 위의 코드는 Forward pass를 구현하는 부분이다. Input data에 대해 각 class의 score를 계산한다. 결과를 score변수에 저장한다. score변수는 NxC행렬이다. 위의 코드의 계산 과정을 표현하면 아래와 같다.
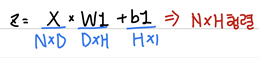
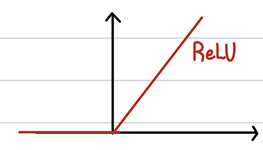
이렇게 계산한 z행렬을 ReLU함수에 대입한다. 0보다 작은 값들은 이 함수에 의해 모두 0으로 대체된다.

##########################################################################
# TODO: Finish the forward pass, and compute the loss. This should include
# both the data loss and L2 regularization for W1 and W2. Store the result
# in the variable loss, which should be a scalar. Use the Softmax
# classifier loss. So that your results match ours, multiply the
# regularization loss by 0.5
##########################################################################
# compute softmax probabilities
out = np.exp(scores) # (N, C)
out /= np.sum(out, axis=1).reshape(N, 1)
# compute softmax loss
loss -= np.sum(np.log(out[np.arange(N), y]))
loss /= N
# L2 regularization
loss += 0.5 * reg * (np.sum(W1**2) + np.sum(W2**2))
##########################################################################
# END OF YOUR CODE
##########################################################################
Forward pass를 끝내고, 최종적으로 loss를 계산하는 부분이다. Data loss를 계산하고, W1, W2를 위해 L2 regularization을 계산한다. Loss function은 softmax를 사용한다. Regularization을 하는 식은 아래와 같다. 이때 R(W)앞에 곱하는 변수는 0.5로 정한다. Reg는 하이퍼 파라미터로 조정이 가능하다.
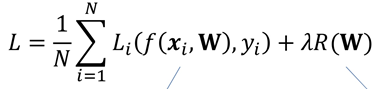
먼저, softmax함수를 이용하기 위해 scores각 원소에 exponential연산을 취한다. 그 다음 이 결과(각 원소들)를 모든 클래스들의 각 score에 exponential을 취한 것을 모두 더한 값으로 나누어 준다. 이렇게 softmax porobability를 구할 수 있다. 최종 결과로 각 샘플별로 각 클래스에 대한 확률 값이 구해진out변수에 NxC의 형태로 저장된다.
아래의 식은 softmax loss function이다.
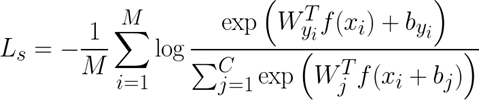

위 식에서 M은 위의 코드의 N에 해당한다. 이것을 구현한 부분이 위의 softmax function을 구현한 부분이다. 각 out의 각 열에서 y만큼(정답 클래스의 레이블) 떨어진 곳의 원소에 마이너스 로그를 취한 뒤 모두 더한 다음 N으로 나누어 준다. 그리고 그 아랫부분은 L2 Regularization을 구현한다. 0.5에 reg를 곱하고 W1, W2의 각 원소의 값을 제곱해서 모두 더한 값을 곱한다.
# Backward pass: compute gradients
grads = {}
##########################################################################
# TODO: Compute the backward pass, computing the derivatives of the weights
# and biases. Store the results in the grads dictionary. For example,
# grads['W1'] should store the gradient on W1, and be a matrix of same size
##########################################################################
# back propagation
dout = np.copy(out) # (N, C)
dout[np.arange(N), y] -= 1
dh = np.dot(dout, W2.T)
dz = np.dot(dout, W2.T) * (z > 0) # (N, H)
# compute gradient for parameters
grads['W2'] = np.dot(h.T, dout) / N # (H, C)
grads['b2'] = np.sum(dout, axis=0) / N # (C,)
grads['W1'] = np.dot(X.T, dz) / N # (D, H)
grads['b1'] = np.sum(dz, axis=0) / N # (H,)
# add reg term
grads['W2'] += reg * W2
grads['W1'] += reg * W1
##########################################################################
# END OF YOUR CODE
##########################################################################
Back-Propagation을 구현하는 부분이다. 각 가중치 값에 학습율*(손실함수를 가중치로 각 가중치 로 미분한 값)을 빼 준다. 이를 대략적인 식으로 나타내면 아래와 같다.
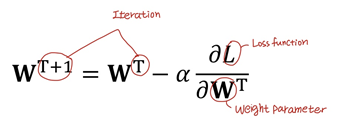
먼저 dout에 out의 값을 복사한 후, 각 원소에 1을 각각 빼준다. 그리고 dout과 W2의 Transpos를 곱한 결과를 dh에 저장한다.
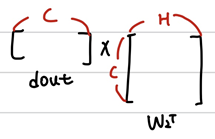
마찬가지로 다른 값들도 곱해서 grads dictionary에 넣어준다.
(3) def train(self, X, y, X_val, y_val, learning_rate=1e-3, learning_rate_decay=0.95, reg=1e-5, num_iters=100, batch_size=200, verbose=False):
#########################################################################
# TODO: Create a random minibatch of training data and labels, storing
# them in X_batch and y_batch respectively.
#########################################################################
random_idxs = np.random.choice(num_train, batch_size)
X_batch = X[random_idxs]
y_batch = y[random_idxs]
#########################################################################
# END OF YOUR CODE
#########################################################################
np.random.choice는 표본의 무작위 추출을 위해 사용하는 함수이다. 0부터 num_train까지의 수중 랜덤으로 batch_size개의 정수를 추출한다. 이렇게 추출된 정수들을 인덱스로 하여, 그에 해당하는 데이터를 X_batch와 y_batch에 각각 넣어준다.
#########################################################################
# TODO: Use the gradients in the grads dictionary to update the
# parameters of the network (stored in the dictionary self.params)
# using stochastic gradient descent. You'll need to use the gradients
# stored in the grads dictionary defined above.
#########################################################################
self.params['W2'] -= learning_rate * grads['W2']
self.params['b2'] -= learning_rate * grads['b2']
self.params['W1'] -= learning_rate * grads['W1']
self.params['b1'] -= learning_rate * grads['b1']
#########################################################################
# END OF YOUR CODE
#########################################################################
위의 loss함수에서 grads를 계산했다. 이렇게 계산한 gradient를 learning_rate와 곱한 뒤 weight, bias에 각각 빼 주어 값을 업데이트 한다. 이과정을 식으로 표현하면 아래와 같다.
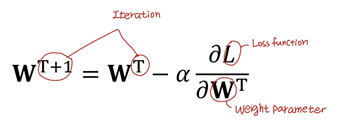
(4) def predict(self, X):
##########################################################################
# TODO: Implement this function; it should be VERY simple!
##########################################################################
z = np.dot(X, params['W1']) + params['b1']
h = np.maximum(z, 0)
out = np.dot(h, params['W2']) + params['b2']
y_pred = np.argmax(out, axis=1)
##########################################################################
# END OF YOUR CODE
##########################################################################
학습된 파라미터들을 이용해서 test하는 과정이다. 마찬가지로 2 layer이다. argmax함수를 사용하여 out의 각 원소중 값이 제일 큰 index를 예측값으로 한다.
<2> neural_net.ipynb
<Result>
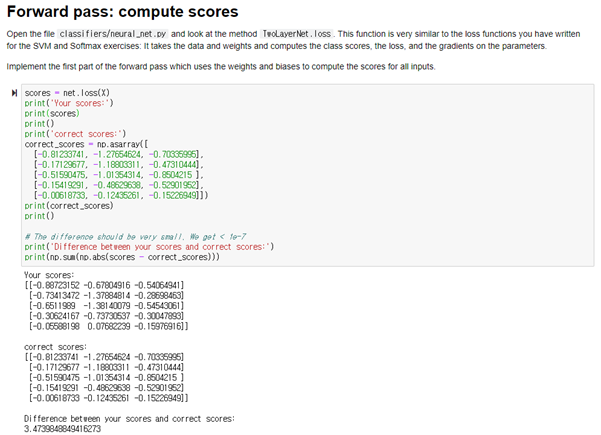
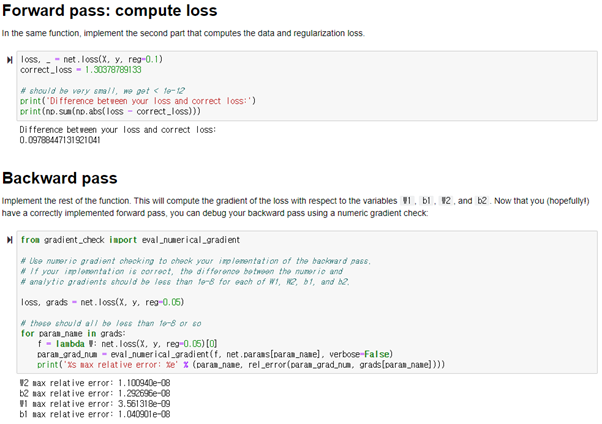
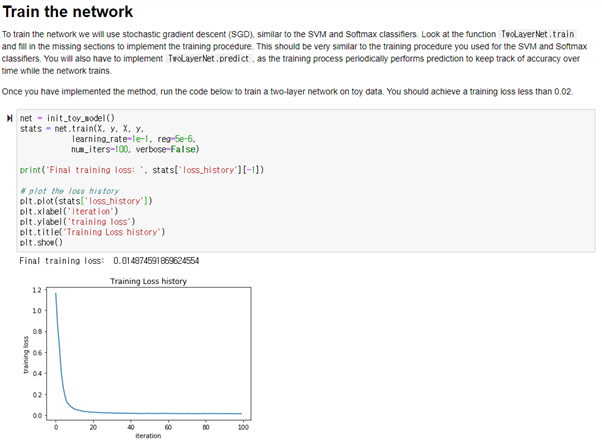
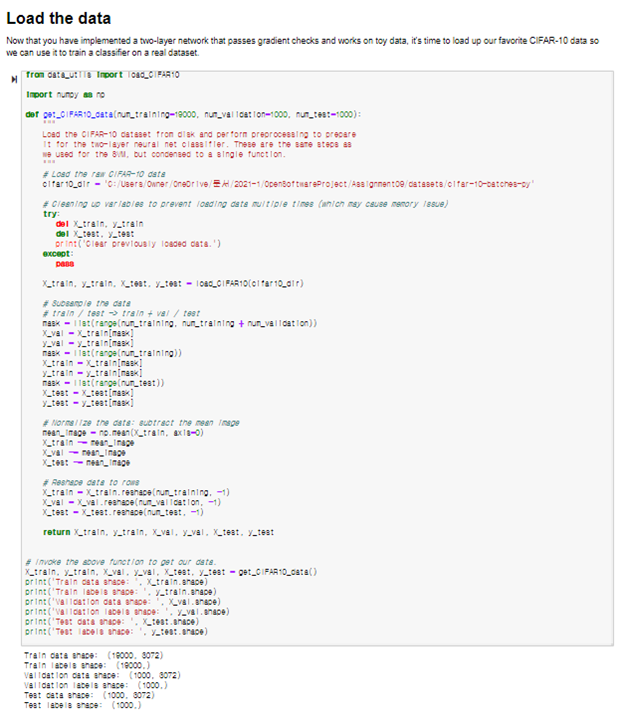
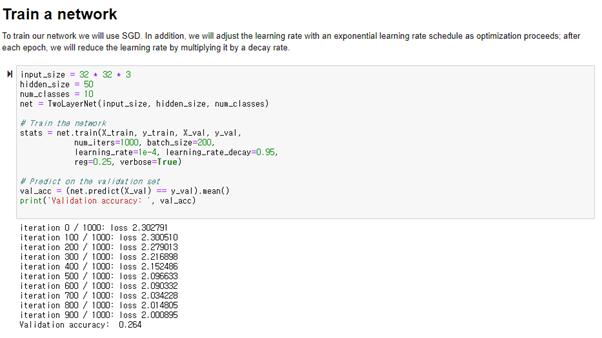
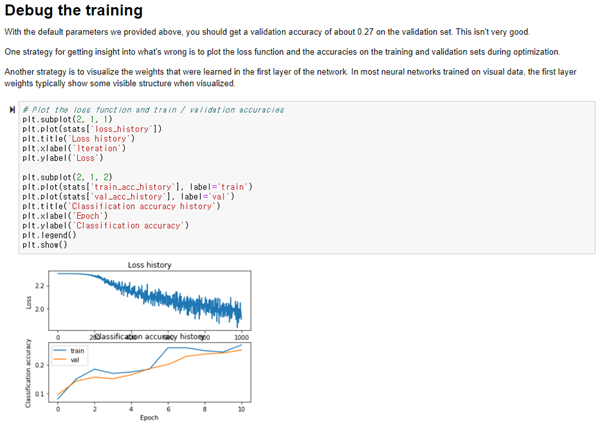
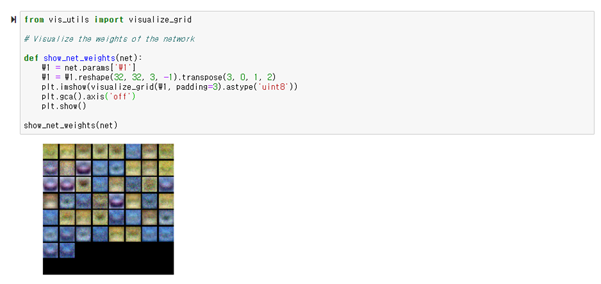
Inline Question: Now that you have trained a Neural Network classifier, you may find that your testing accuracy is much lower than the training accuracy. In what ways can we decrease this gap? Select all that apply.
1. Train on a larger dataset.
2. Add more hidden units.
3. Increase the regularization strength.
4. None of the above.
Answer: 1, 3: This is happened due to the over-fitting on training data. Therefore, we should generalize model in order to decrease the gap between the traing and testing accuracy. To decrease this gap, first, we can use larger dataset to consider more broader spactrum of data so that it can predict similarly on training and test data. Second, we can Increase the regularization strength to avoid over fitting. Decreasing overall values of weights can help to avoid over-fitting. However, if we use more hidden units, it can lead to over-fitting. Therefore in deeplearning, we usually use drop to avoid this. "